Combinación de Funciones

En esta seccion se estudian diferentes formas de combinar funciones para construir otras.

Suma, Diferencias, Productos y cocientes

Dos funciones f y g se pueden combinar para formar nuevas funciones f+g, f-g, f(g) y
f/g de una manera similar a la forma en que se suma, resta multiplicacion y se dividen numeros reales. Se define la informacion f+g por:
(f+g)(x) = f(x)+g(x)


Ej. 1.
f(x)= 2x-4
g(x)= x-2

(f+g)(x)=
=2x-4+x-2
= 2x+x-4-2
(f+g)(x)= 3x-6


2(f-g)(x)=f(x)-g(x)
f(x)=7x-2
g(x)=4x+5

(f-g)(x)= 7x-2-(4x+5)
= 7x-2-4x-5
(f-g)(x)= 3x-7


3.(fg)(x)= [f(x)][g(x)]
f(x)=7x-2
g(x)=4x+5

(fg)(x)=(7x-2)(4x+5)
=28x^2+35x-8x-10
(fg)(x)=28x^2+27x-10


4.(f/g)(x)
f(x)=2x-4
g(x)=x-2

=2x-4/x-2
=2 (x-2)/(x-2)
*(x-2) se cancelan.
(f/g)(x)=2

Funciones de Dominio Partido

Continuamos graficando funciones pero con restricciones en el dominio, conocido como dominio partido. El mismo indica un valor de la variable independiente y lo manipula segun la funcion; entre estas: mayor o igual, menor o igual, menor que, mayor que y no es igual. Estas desigualdades muestran en la grafica cuales puntos se pueden o cuales no. Tambien ayudan a comprobar cuales resultados de la tabla de valores son ciertos.

Funciones Crecientes y Decrecientes

En la clase de hoy empezamos a discutir un tema nuevo, el maestro dio par de ejemplos. A continuacion ira la informacion discutida.

*Tasa de cambio promedio
-Las funciones emplean con frecuencia para modelar cantidades cambiantes.
-Es importante saber donde sube la grafica y donde baja.


*Solucion:
-f es creciente en: [a]
-f es decreciente en: [b]


*Definicion:
- f es creciente en un intervalo 1 si f(x1)
- f es decreciente en un intervalo 1 f(x1)>f(x2) siempre que x1

Funciones pares e impares

Sea (f) una funcion:
-----> (f) es por si f(-x) = f(x) para toda (x) en el dominio de (f).
-----> (f) es impar si f(-x)=-f(x) para todo (x) en el dominio de (f).

Ejemplo #1:
Impar:



*La grafica de una funcion impar el simetrica respecto al origen.

Ejemplo #2:
Par:

http:

*La grafica de una funcion par es simetrica respecto al eje de Y.

IMPORTANTE:
Cuando los signos cambian la funcion sera impar, ahora si se quedan de la misma forma al original este sera par; Cuando la X es negativa entonces no TIENE SIMETRIA.

Ejemplo:
f(x)= x(x^4-x^2)+4 ****lAS X SON NEGATIVAS POR LO TANTO NOTIENE SIMETRIA****
=-x((-x)^4-(-x)^2)+4
=-x(x^4-x^2)+4


Ejemplo #3:

f(x)=x^3+2x
=(-x)^3+2(-x)
=-x^3-2x



Ejemplo #4:

f(x)=X^2- [x]
=(-x)^2-[x]
=x^2+ [x]



G.M.R.S

Transformacion de Funciones

Ejemplo #1:

f(x) =2x^2



Ejemplo #2:

f(x)= X^2





Ejemplo #3:



*Si la grafica es mayor que (1) se va a pegar al eje de Y.
*Si la grafica es menor que (1) se despega del eje de Y.


G.M.R.S

Transformacion de Funciones

Las transformaciones son : desplazamientos , reflexion y estiramiento.

Desplazamientos Verticales :

* Para graficar y=f(x)+c , desplace c unidades hacia arriba la graficar de y=f(x)

* Para graficar y=f(x)-c , desplace c unidades hacia abajo la graficar de y=f(x)

Observa que la gráfica de y = x² + 2 sube dos unidades desde el origen

y la gráfica de y = x² - 3 baj

a tres unidades desde el origen.

Desplazamientos Horizontales :

* Para graficar y=f(x-c) desplace la grafica y=f(x) a la derecha c unidades.

* Para graficar y=f(x=c) desplace a la grafica y=f(x) a la izquierda c

unidades .

Observa que la gráfic

a de y = ( x + 2)² se mueve dos unidades hacia la izquieda y la gráfica de y = (x - 2)² se mueve dos unidades hacia la derecha.

Asintota :

asintota vertical

asintota horizontal

Reflexion de la grafica

* Para graficar y= -f(x) , refleje la grafica de y=f(x) en el eje de X.

* Para graficar y=f(-x),refleje la grafica de y=f(x) en el eje de Y.

Cuando la gráfica de y = f(x) es reflejada en el eje de x. Por ejemplo: si f(x) = x² entonces g(x) = -x² es una reflexión de f(x) = x². Veamos las gráficas ...

Función Parte Entera

Hoy el maestro explico sobre las funciones de parte entera, dio un ejemplo y ejercicios.

La función parte entera de cualquier numero x es el entero mas grande que es menor o igual a x.

La parte entera de x esta denotada por [|x|]

Evalúa las siguientes expresiones.

a.[|2.3|] b.[|1.9|] c. [|0.1|] d.[|-0.3|]

      2          1            0          -1

e.[|-3.7|] f.[|3|] g.[|-2|] h.[|-0.999|]

      -3       3        -2           -1

Graficas de Funciones Basicas

Hoy estabamos familiarizandonos con las graficas de las funciones mas basicas, que de base, debemos de memorizarlas para hacer el proceso de aprendizaje mas facil en lo que es la introduccion al precalculo. Esta es la continuacion de las otras graficas que tocamos el 30 de agosto.

1. Funcion Cubica

Df=(-∞,∞)

Rf=(-∞,∞)

2. Funcion de Valor Absoluto

Df=(-∞,∞)

Rf=[0,∞)

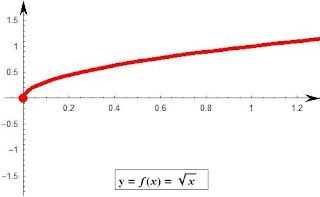
3. Funcion Raiz Cuadrada

Df=[0,∞)

Rf=[0,∞)

4. Funcion Racional

Df=(-∞,0)U(0,∞)

Rf=(-∞,0)U(0,∞)

5. Funcion Raiz Cubica

Df=(-∞,∞)

Rf=(-∞,∞)

6. Funcion Constante

f(x) = b

Df=(-∞,∞)

Rf=[b]

Graficas de Funciones

El dia 30/agotso/2011 el maestro nos empezo a dar una breve descripcion de par de tipos de graficas junto a sus funciones, dominios y rangos. Las cuales son las siguientes:

A. Funcion Identidad:

. f(x)= x

B. Funcion Lineal:

f(x)= mx+b

C. Funcion Cuadratica:

René Descartes

La Haye, Francia, 1596 - Estocolmo, Suecia, 1650) Filósofo y matemático francés. René Descartes se educó en el colegio jesuita de La Flèche (1604-1612), donde gozó de un cierto trato de favor en atención a su delicada salud.
Obtuvo el título de bachiller y de licenciado en derecho por la facultad de Poitiers (1616), y a los veintidós años partió hacia los Países Bajos, donde sirvió como soldado en el ejército de Mauricio de Nassau. En 1619 se enroló en las filas del duque de Baviera; el 10 de noviembre, en el curso de tres sueños sucesivos, René Descartes experimentó la famosa «revelación» que lo condujo a la elaboración de su método. Los cinco primeros años los dedicó principalmente a elaborar su propio sistema del mundo y su concepción del hombre y del cuerpo humano, que estaba a punto de completar en 1633 cuando, al tener noticia de la condena de Galileo, renunció a la publicación de su obra, que tendría lugar póstumamente.
En 1637 apareció su famoso Discurso del método, presentado como prólogo a tres ensayos científicos. Descartes proponía una duda metódica, que sometiese a juicio todos los conocimientos de la época, aunque, a diferencia de los escépticos, la suya era una duda orientada a la búsqueda de principios últimos sobre los cuales cimentar sólidamente el saber. El método cartesiano, que Descartes propuso para todas las ciencias y disciplinas, consiste en descomponer los problemas complejos en partes progresivamente más sencillas hasta hallar sus elementos básicos, las ideas simples, que se presentan a la razón de un modo evidente, y proceder a partir de ellas, por síntesis, a reconstruir todo el complejo, exigiendo a cada nueva relación establecida entre ideas simples la misma evidencia de éstas. Los ensayos científicos que seguían, ofrecían un compendio de sus teorías físicas, entre las que destaca su formulación de la ley de inercia y una especificación de su método para las matemáticas. Los fundamentos de su física mecanicista, que hacía de la extensión la principal propiedad de los cuerpos materiales, los situó en la metafísica que expuso en 1641, donde enunció así mismo su demostración de la existencia y la perfección de Dios y de la inmortalidad del alma. El mecanicismo radical de las teorías físicas de Descartes, sin embargo, determinó que fuesen superadas más adelante.
Pronto su filosofía empezó a ser conocida y comenzó a hacerse famoso, lo cual le acarreó amenazas de persecución religiosa por parte de algunas autoridades académicas y eclesiásticas, tanto en los Países Bajos como en Francia. En 1649 aceptó la invitación de la reina Cristina de Suecia y se desplazó a Estocolmo, donde murió cinco meses después de su llegada a consecuencia de una neumonía. Descartes es considerado como el iniciador de la filosofía racionalista moderna por su planteamiento y resolución del problema de hallar un fundamento del conocimiento que garantice la certeza de éste, y como el filósofo que supone el punto de ruptura definitivo con la escolástica.

-GMRS