Funciones Racionales

Ejemplo #1:
f(x)=2/x²-4

1. DF- (∞,-2)u(-2,2)u(2,∞)

x²-4≠0
x²≠4
√x²≠ ±√4
x≠±2

2. asintotas verticales:

x²-4=0
√x²=±√4
x=±2
3.Tablas de valores:
x-->-2-
x y
-4 0.16
-3 0.4
-2.5 0.88
-2.3 1.5
-2.2 2.4
-2.1 4.9

x-->-2-2+
x y
-1 -0.67
0 -0.5
.1 -0.67
-1.5 -1.14
1.5 -1.14
-1.7 -1.8
1.7 1.8
-1.9 -5.1
1.9 5.1

x-->2+
x y
2.1 4.9
2.2 2.4
2.3 1.5
2.5 0.88
3 0.4
4 .16


4.Grafica:



Asintotas Horizontales:
R(X)=(AnX^n+An-1X^n-1….A1X+Ao)/(bmX^m+bm-1X^m-1…b1X-bo)

Las asintotas Horizontales se obtienen:
a. Si nb. Si n=m entonces R tiene asintota horizontal y=an/bm
c. Si n>m entonces R no tiene asintota horizontal, tiene asintota oblicua.

ejemplo:
3x²/6x² *los exponentes son iguales por lo tanto se pueden dividir*

=3/6
=1/2
y=1/2

Funciones Racionales

Una funcion racional es una funcion en la forma r(x)=p(x),donde Q(x) ≠ 0.

Ej.1. f(x)=1/x:Q(x) x≠0.

2.h(x)=1/(x+2); x≠ -2

3.g(x)=x+8/x^2-9 ; x ≠ ± 3

Asintotas verticales , horizontales u oblicuas.

-Asintota vertical h(x)=1/x+2

Df= (-∞,-2) U (-2,∞)

-Asintota Vertical

x+2=0

x=-2

x-->-2+

x y

-----------

-5 -.33

-4 -.5

-3 -1

-2.2 -5

-2.5 -2

x--> -2+

x y

--------------------

-1.5 2

-1.7 3.3

-1.8 5

-1 1

0 0.5

2 0.25

3 0.2

4 0.16

Luego de tener las tablas de valores y haber marcado la asintota vertical procedemos a graficar .

Por ejemplo f(x)=1/1-x con su asintota vertical marcada quedaria de esta forma.

Teorema de ceros conjugados

Si el polinomio P tiene coeficientes reales, y si el numero complejo Z es un cero de P, entonces su complejo conjugado Z es también un cero de P.

Ej. 1)Escribe un polinomio de grado 3 cuyos cerros son: 1,-5,6

X1= 1 => X-1
X2=-5 => X+5
X3= 6 => x-6

f(x)=(x-1)(x+5)(x-6)
= x^2+5x-x-x(x-6)
=(x^2+4x-5)(x-6)
= x^3-6x^2+4x^2-24x-5x+30
f(x)= x^3-2x^2-29x+30

2)Escribe un polinomio de grado 3 cuyos ceros son 3, -2i

x1= 3 => x-3
x2= -2i => x+2i
x3= 2i => x-2i

f(x)= (x-3)(x+2i)(x-2i)
= (x-3)(x^2+4)
= x^3+4x-3x^2-12
f(x)= x^3-3x^2+4x-12


3) Escriba in polinomio de grado 4 cuyos ceros son: 1,-2i y 1 de multi 2.

x1= 1-2i => x-(1-2i)
x2= 1+2i => x-(1+2i)
x3= 1 => 1
x4= 1 => 1

[(x-1)^2-2i][(x-1)+2i]
(x-1)^2 -(2i)^2
x^2-2x+1+4
x^2-2x+5


f(x)=(x-1)^2(x^2-2x+5)
= (x^2-2x+1)(x^2-2x+5)
= x^4-2x^3+5x^2-2x^3+4x^2-10x+x^2-2x+5
f(x)= x^4-4x^3+10x^2-12x+5


4)Encuentre un polinomio de grado 3 cuyos ceros son 3-i y 1/2

x1=1/2 => x=(1/2) = 2x=1=> (2x-1)
x2=3-i =>x-3+i
x3=3+i =>x+3-i


f(x)= (2x-1)(x-3-i)(x-3+i)
= (2x-1)(x^2-6x+10)
= 2x^3-12x^2+20x-x^2+6x-10
f(x)= 2x^3-13x^2+26x-10




Biografías

Carl Friedrich Gauss



Carl Friedrich Gauss(30 de abril de 1777, Brunswick – 23 de febrero de 1855, Göttingen), fue un matemático, astrónomo y físico alemán que contribuyó significativamente en muchos campos, incluida la teoría de números, el análisis matemático, la geometría diferencial, la geodesia, el magnetismo y la óptica. Considerado «el príncipe de las matemáticas» y «el matemático más grande desde la antigüedad», Gauss ha tenido una influencia notable en muchos campos de la matemática y de la ciencia, y es considerado uno de los matemáticos que más influencia ha tenido en la Historia. Fue de los primeros en extender el concepto de divisibilidad a otros conjuntos.
Gauss fue un niño prodigio, de quien existen muchas anécdotas acerca de su asombrosa precocidad. Hizo sus primeros grandes descubrimientos mientras era apenas un adolescente y completó su magnum opus, Disquisitiones Arithmeticae a los veintiún años (1798), aunque no sería publicado hasta 1801. Fue un trabajo fundamental para que se consolidara la teoría de los números y ha moldeado esta área hasta los días presentes.


Leonhard Euler




Leonhard Paul Euler(Basilea, Suiza, 15 de abril de 1707 - San Petersburgo, Rusia, 18 de septiembre de 1783), conocido como Leonhard Euler, fue un matemático y físico suizo. Se trata del principal matemático del siglo XVIII y uno de los más grandes de todos los tiempos.
Vivió en Rusia y Alemania la mayor parte de su vida y realizó importantes descubrimientos en áreas tan diversas como el cálculo o la teoría de grafos. También introdujo gran parte de la moderna terminología y notación matemática, particularmente para el área del análisis matemático, como por ejemplo la noción de función matemática. Asimismo se le conoce por sus trabajos en los campos de la mecánica, óptica y astronomía.
Euler ha sido uno de los matemáticos más prolíficos, y se calcula que sus obras completas reunidas podrían ocupar entre 60 y 80 volúmenes. Una afirmación atribuida a Pierre Simon Laplace expresa la influencia de Euler en los matemáticos posteriores: Lean a Euler, lean a Euler, él es el maestro de todos nosotros.


Évariste Galois




Évariste Galois (25 de octubre de 1811 - 31 de mayo de 1832) fue un matemático francés nacido en Bourg-la-Reine. Mientras aún era un adolescente, fue capaz de determinar la condición necesaria y suficiente para que un polinomio sea resuelto por radicales, dando una solución a un problema que había permanecido sin resolver. Su trabajo ofreció las bases fundamentales para la teoría que lleva su nombre, una rama principal del álgebra abstracta. Fue el primero en utilizar el término "grupo" en un contexto matemático. La teoría constituye una de la bases matemáticas de la modulación CDMA utilizada en comunicaciones y, especialmente, en los Sistemas de navegación por satélite, como GPS, GLONASS, etc.

Ceros complejos y el teorema fundamental de Algebra

-Teorema fundamental de Algebra:

• Todo polinomio:

p(x)=Anx^n+Aan-1X^n-1+...A1X+A0

donde: n > o = 1, An no = 0

-Teorema de la factorizacion completa:

• Si p(x) es un polinomio de grado n > o = 1, entonces existen numeros complejos a, c1, c2...cn con a no = 0 tal que:

p(x)=a(x-c1)(x-c2)...(x-cn)

• i^2 = -1

Ejemplo:

1) f(x)=x^3+x^2+9x+9

=(x^3+X^2)+(9x+9)

=x^2(x+1)+9(x+1)

=(x+1)(X^2+9)

=x^2+9=0

x1=-1

x2=3i

x3=-3i

Regla de los Signos de Descartes

Regla de los Signos de Descartes:

• El numero de ceros reales positivos es igual # de variaciones en el signo de los coeficientes diferentes de ceros de f(x)


• El # de ceros reales es igual al # de variaciones en signos de los coeficientes de cero de f(-x)

f(x)= x^3+2x^2-5x-6
f(-x)= -x^3+2x^2+5X-6

0=1 positivo

0= 2 negativo

p/q= factores de ultimo termoni/factores del primer termino

p/q= ±1±2±3±6/±1

Los posibles ceros son: ±1±2±3±6

-1 I 1 2 -5 -6
I
I -1 -1 6
I____________
-3 I 1 1 -6 0
I
I -3 6
I___________
1 -2 0

X-2=0
x=2

x1=-1

x2=-3

x3=2

f(x)=(x+1)(x+3)(x-2)

Funciones Polinomicas

-Teorema de factorizacion completa-:
Si p(x) es un polinomio de grado n>0 , entonces existen numeros complejos a,c,C2.....Cn(con a no es igual a 0)

p(x)= a(x-c)(x-C2).....(x-Cn)

Estos ceros no necesitan o tienen que ser distintos. Si el factor x-c aparece K aveces en la factorizacion completa del polinomio p(x), decimos que c es un cero de multipicidad K.

Para Para cada funcion polinomial:
a. halle las raices reales.
b. Halle el intercepto en Y.
c. Determine los intervalos donde la grafica esta sobre el eje de X.
d.Determine los intervalos donde la grafica esta debajo del eje de X.
e. trace un bosquejo de la grafica F.



Ejemplo:
4x^3-8x^2
-4x^2(x+2)
-4x^2/-4=0/4------> x1=0 x2=0


x+2=0------>x3=-2

f(x)>0(infinito,-2)
f(x)<0(-2,0)u(0,infinito)

Intercepto en x:(0,0)(2,0)
Intercepto en Y:(0,0)


Grafica:

Funciones Polinomiales

Grafica de una Funcion Polinomial

- Grado del polinomio : n

- Multiplicidad par Grafica toca el eje de X

- Multiplicidad impar Grafica cruza del eje de X

- Entre ceros , la grafica puede estar debajo o encima del eje de X : depende del valor del numero del intervalo.

-Compartimiento terminal para grado impar .Si el coeficiente principal es positivo,comienza abajo termina arriba.Si , es negativo , comienza arriba , termina abajo .

-Comportamiento terminal para grado par : si el coeficiente principal es positivo , comienza arriba termina arriba , si es negativa comienza abajo termina abajo.

Funciones Polinomoales

f(x)= x^3-x
=x(x^2-1)
=x(x+1)(x+1)

0=x(x+1)(x-1)

x1=0 x2=1 x3=-1




tabla de valores

X
-2
-0.5
0.5
2
-1
0
1
1.5
-1.5

Y
-6
0.377
-0.37
6
0
0
0
1.8
-1.8

Funciones Polinomiales

f(x)=An+X^n+An1X^n1+An2X^n2+...
donde An, An1... son numeros reales y n es entero no negativo. El dominio lo constituyen todos los numeros reales, osea, de negativo infinito a positivo infinito. Una funcion polinomial es una cuya regla esta dada por un polinomio en una variable. El grado de una funcion polinomial es el grado del polinomio en una variable, en otras palabras, el numero del exponente mas grande en una variable.

Ej:
f(x)=3x^4-2x^3+8x^2+7x+1
f(x)=-6x^2-2x+1
f(x)=x^5-3x^2+1

Graficas de una funcion polinomial:
f(x)=ax^n

• Cuando n es impar y a > 0 comienza de abajo hacia arriba.
• Cuando n es impar y a < 0 comienza de arriba hacia abajo.
• Cuando n es par y a > 0 comienza arriba y termina arriba.
• Cuando n es par y a < 0 comienza abajo y termina abajo.
  

Problemas de Aplicacion

En estos dias empezamos con los problemas verbales uno de ellos es:

Caida Libre - Funcion de Posicion

A un tiempo cero (t=0) un clavadista se impulsa a una velocidad de 16pies/seg desde una plataforma que se encuentra a una altura de 32 pies sobre el agua.

s(t)= -1/2gt^2 + vot +so

g= 9.8m/s o 32pies

t= tiempo

vo= velocidad inicial

so+ posicion inicia


a) ¿Cual es la funcion que define la trayectoria del clavadista?

s(t)= -1/2(32)t^2 + 16t +32

s(t)= -16t^2 +16t + 32

b)¿Cual es la altura maxima que alcanza el clavadista?

S(0.5)=-16(.5)^2+16(.5)+32S(.5)
h max=36pies

c)¿Cuanto tiempo le alcanzara al clavadista alcanzar la altura maxima?

t=-b/2a

t=-16/2(-16)

t=.5 segundos

d)¿Cuando el clavadista toca o llega al agua?

0=-16t^2+16t+32

0/-16=-16/-16 (t^2-t-2) *se cancelan los -16

0= (t+1) (t-2)

t+1=0

t1=0/1 N/A

t-2=0

t2=2secs.

e)¿A que altura se encontraba el clavadista despues de 1sec. de haberse lanzado?

s(t)= -16t^2 +16t + 32

s(1)= -16(1)^2+16(1)+32

*SMJ

Funciones Cuadraticas

-Forma Estandar-ejemplo #1:

f(x)= -2x^2-4x+2
=(-2x^2-4x)+2
=-2(x^2+2x)+2
=-2(x^2+2x+1-1)+2
=-2(x^2+2x+1)+2+2
=-2(x+1)^2+4
f(x)= -2(x+1)^2+4

Una de las formulas que se utilizan en estos ejercicios es:
(b/2)^2

y= -2x^2-4x+2
y= -2(0)^2-4(0)+2
y= 0-0+2
y=2

0= -2(x+1)^2+4
-4/-2= -2(x+1)^2/_2 -------> los negativo 2 se cancelan
±√2=√(x+1)^2
±√2=x+1
-1+√2= 0.41
-1-√2= -2.41


x= -b±√b^2-4ac/2a
x=4±√(-4)^2-4(-2)(2)/2(-2)
x=4±√16+16/-4
x=4±√32/-4
x=4±√16.2/4
x=4±4√2/-4
x=4(1±√2)/-4 -------> se cancelan los 4
x=1±√2
x1= 1+√2= 2.41
x2=1-√2=-.41


Vertice: (-1,4)
eje de simetria: x=-1
concavidad: a < 0 es concava hacia abajo intercepto en y: (0,2) intercepto en x: (0.41,0) (-2.41,0) Tabla De Valores: x Y -1 4 0 2 0.41 0 -2.41 0 -2 2 -3 4 1 -4 -3.5 -8.5 1.5 -8.5

G.M.R.S

Funcion Cuadratica en su Froma General

La forma general de una función cuadrática es; f(x)= x²+bx+c , donde a,b y c son

números reales.

Ejemplo de forma general :

f(x)= 3x²+7x-6

Concavidad= Cóncava hacia arriba

Vértice ( -1.17, -10.1 )

x=-b/2a

=-7/2(3)

=-1.17

y=f(-1.17)=3(-1.17)²+7(-1.17) -6

=4.11-8.19-6

=-10.1

Eje de simetría x = 1.17

Interceptos en el eje de x ( 0.67 , 0 ) y ( - 3 , 0 )

Este es un ejemplo de la funcion es su forma general , de cada ejercicio se saca tambien sus valores para proceder a demostrar la funcion en su manera grafica con sus valores ya obtenidos.

Eje de Simetria

El eje de simetría es la recta que pasa por el vertice de una parabola que divide la
parábola en dos mitades congruentes.

La función cuadrática f(x)=a(x-h)²+k tiene el eje de simetría en x=k




Funciones Cuadráticas
Forma General
f(x)=a²+bx+c

Forma Estándar
f(x)=a(x-h)²+k

Ej. f(x)=x²+2x-8 (b/2)²
=(x²+2x)-8 (2/2)²= 1
=(x²+2x+1-1)-8
=(x²+2x+1)-8-1
=(x²+2x+1)-9
=(x+1)²-9

a)Vertice=(-1-9)
b)Eje de simetria= x=-1
c)Int en y= (0,-8)
(x=0)

f(x)=(x+1)²-9
y=(0+1)²-9
y=1-9
y=-8

d)Int en x x1=(2,0)
(y=0) x2=(-4,0)


0=(x+1)²-9
9=(x+1)²
+-√9=√(x+1)²
+-3=x+1
-1+-3=x
x=-1+3 x=-1-3
x=2 x=-4

e) Concavidad= a>0 U

Funcion Cuadratica

Una funcion cuadratica es una funcion que puede ser escrita en la forma:

Forma Estandar:

f(x)=a(x-h)^2+k donde a no puede ser 0.

Forma General:

ax^2+bx+c=0

La grafica de una funcion cuadratica tiene forma de U y se conoce como parabola.

Vertice de una Parabola:

• Si una parabola abre hacia arriba tiene un punto minimo.

• Si una parabola abre hacia abajo, tiene un punto maximo.

• Este punto mas bajo o mas alto es el vertice de la parabola.
• La forma del vertice de una funcion cuadratica es f(x)=a(x-h)^2+k.
• El vertice de una parabola es (h,k).

f(x)=a(x-h)^2+k

• a - indica reflexion del eje de x,y/o una compresion/estiramiento vertical.
• h - indica translacion horizontal.
• k - indica una translacion vertical.

Tomar en cuenta a la hora de solucionar:

• Vertice (h,k)
• Eje de Simetria
• Intercepto en y
• Intercepto en x (discriminante)
• Concavidad
• Tabla de Valores
• Grafica

Funciones Uno a Uno & Sus Inversas

Funciones Uno a Uno
En la clase de hoy hablamos y duscutimos un tema nuevo, el cual es bastante facil que es: Funciones uno a unos & funciones Inversas.


Def: De una funcion uno a uno, una funcion con dominio A se conoce como uno a uno, si no hay dos elementos de A que tengan el mismo rango, esto es:
f(x1) no es igual f(x2) siempre que x1 no sea igual que x2.


f es uno a uno


g no es funcion uno a uno



*Prueba de la recta horizontal
-Una funcion es uno a uno si ninguna recta horizontal interseca su grafica mas de una vez. NO es funcion uno a uno.






Funciones Inversas

Las funciones uno a uno son importantes porque estas tienen funciones inversas con la siguinete definicion:
-Sea f una funcion uno a uno con dominio A y rango B. Entonces su funcion inversa f^-1 tiene dominio B y rango A esta definida por: f^-1= x ► f(x)= y
ej:
f(x)=y

y=3x-5

x= 3y-5

x+5/3=3y/3 *se cancelan los 3

f^-1(x)= x+5/3

*smj

Comprension De Funciones

Dadas dos funciones (f) y (g), la funcion compuesta (f) o (g) tambien conocida como composicion de (f) y (g) esta definida por:
p.193

a. (f o g)(x)= f(g(x))
b. (g o f)(x)= g(f(x))

Ejemplo 1:
f(x)= 5X² -3
g(x)= x+5

a. (f o g)(x)
= 5(x+5)²-3
= 5(X²+10x+25)-3
= 5X²+50x+125-3
= 5X²+50x+122

b. (g o f)(x)= 5X²-3+5
= 5X²+2

Ejemplo 2:
f(x)= √x
g(x)= X²+1

a. (f o g)(x)
=√X²+1

b. (g o f)(x)
=(√X)²+1
= x+1
Ejemplo 3:
(g o g)(x)
= X²+1
= (X²+1)²+1
= x⁴+2x²+1+1
= x⁴+2x²+2

Ejemplo 4:
(f o g o h)(x)
f(x)= 1/x
g(x)= x³
h(x)= X²+2

= 1/x
= 1/x³
= 1/(X²=2)³
= 1/(X²)³+3(X²)²(2)+3(x²)(2)²+2(3)
= 1/x⁶+6x⁴ +12x²+8

G.M.R.S

Combinacion de Funciones y sus Dominios.

La seccion trabajada hoy se baso en la continuacion del tema Combinacion de Funciones y permanecimos familiarizandonos con encontrar las funciones de: f+g,f-g,f(g),f/g.

ejemplo :

f(x)= x³ + 2x²

g(x)=3x²-1

a)x³ + 2x²+3x²-1 f+g(x)

=x³ + 6x²-1

b)x³ + 2x²-3x²+1 f-g(x)

= x³ + x²+1

c)(x³ + 2x²)(3x²+1) f(g)(x)

=3x^5-x³ +6x⁴ -2x²

d)x³ + 2x² /3x²-1 f/g(x)

Dos funciones Fy G se pueden unir para formar nuevas funciones .

Combinación de Funciones

En esta seccion se estudian diferentes formas de combinar funciones para construir otras.

Suma, Diferencias, Productos y cocientes

Dos funciones f y g se pueden combinar para formar nuevas funciones f+g, f-g, f(g) y
f/g de una manera similar a la forma en que se suma, resta multiplicacion y se dividen numeros reales. Se define la informacion f+g por:
(f+g)(x) = f(x)+g(x)


Ej. 1.
f(x)= 2x-4
g(x)= x-2

(f+g)(x)=
=2x-4+x-2
= 2x+x-4-2
(f+g)(x)= 3x-6


2(f-g)(x)=f(x)-g(x)
f(x)=7x-2
g(x)=4x+5

(f-g)(x)= 7x-2-(4x+5)
= 7x-2-4x-5
(f-g)(x)= 3x-7


3.(fg)(x)= [f(x)][g(x)]
f(x)=7x-2
g(x)=4x+5

(fg)(x)=(7x-2)(4x+5)
=28x^2+35x-8x-10
(fg)(x)=28x^2+27x-10


4.(f/g)(x)
f(x)=2x-4
g(x)=x-2

=2x-4/x-2
=2 (x-2)/(x-2)
*(x-2) se cancelan.
(f/g)(x)=2

Funciones de Dominio Partido

Continuamos graficando funciones pero con restricciones en el dominio, conocido como dominio partido. El mismo indica un valor de la variable independiente y lo manipula segun la funcion; entre estas: mayor o igual, menor o igual, menor que, mayor que y no es igual. Estas desigualdades muestran en la grafica cuales puntos se pueden o cuales no. Tambien ayudan a comprobar cuales resultados de la tabla de valores son ciertos.

Funciones Crecientes y Decrecientes

En la clase de hoy empezamos a discutir un tema nuevo, el maestro dio par de ejemplos. A continuacion ira la informacion discutida.

*Tasa de cambio promedio
-Las funciones emplean con frecuencia para modelar cantidades cambiantes.
-Es importante saber donde sube la grafica y donde baja.


*Solucion:
-f es creciente en: [a]
-f es decreciente en: [b]


*Definicion:
- f es creciente en un intervalo 1 si f(x1)
- f es decreciente en un intervalo 1 f(x1)>f(x2) siempre que x1

Funciones pares e impares

Sea (f) una funcion:
-----> (f) es por si f(-x) = f(x) para toda (x) en el dominio de (f).
-----> (f) es impar si f(-x)=-f(x) para todo (x) en el dominio de (f).

Ejemplo #1:
Impar:



*La grafica de una funcion impar el simetrica respecto al origen.

Ejemplo #2:
Par:

http:

*La grafica de una funcion par es simetrica respecto al eje de Y.

IMPORTANTE:
Cuando los signos cambian la funcion sera impar, ahora si se quedan de la misma forma al original este sera par; Cuando la X es negativa entonces no TIENE SIMETRIA.

Ejemplo:
f(x)= x(x^4-x^2)+4 ****lAS X SON NEGATIVAS POR LO TANTO NOTIENE SIMETRIA****
=-x((-x)^4-(-x)^2)+4
=-x(x^4-x^2)+4


Ejemplo #3:

f(x)=x^3+2x
=(-x)^3+2(-x)
=-x^3-2x



Ejemplo #4:

f(x)=X^2- [x]
=(-x)^2-[x]
=x^2+ [x]



G.M.R.S

Transformacion de Funciones

Ejemplo #1:

f(x) =2x^2



Ejemplo #2:

f(x)= X^2





Ejemplo #3:



*Si la grafica es mayor que (1) se va a pegar al eje de Y.
*Si la grafica es menor que (1) se despega del eje de Y.


G.M.R.S

Transformacion de Funciones

Las transformaciones son : desplazamientos , reflexion y estiramiento.

Desplazamientos Verticales :

* Para graficar y=f(x)+c , desplace c unidades hacia arriba la graficar de y=f(x)

* Para graficar y=f(x)-c , desplace c unidades hacia abajo la graficar de y=f(x)

Observa que la gráfica de y = x² + 2 sube dos unidades desde el origen

y la gráfica de y = x² - 3 baj

a tres unidades desde el origen.

Desplazamientos Horizontales :

* Para graficar y=f(x-c) desplace la grafica y=f(x) a la derecha c unidades.

* Para graficar y=f(x=c) desplace a la grafica y=f(x) a la izquierda c

unidades .

Observa que la gráfic

a de y = ( x + 2)² se mueve dos unidades hacia la izquieda y la gráfica de y = (x - 2)² se mueve dos unidades hacia la derecha.

Asintota :

asintota vertical

asintota horizontal

Reflexion de la grafica

* Para graficar y= -f(x) , refleje la grafica de y=f(x) en el eje de X.

* Para graficar y=f(-x),refleje la grafica de y=f(x) en el eje de Y.

Cuando la gráfica de y = f(x) es reflejada en el eje de x. Por ejemplo: si f(x) = x² entonces g(x) = -x² es una reflexión de f(x) = x². Veamos las gráficas ...

Función Parte Entera

Hoy el maestro explico sobre las funciones de parte entera, dio un ejemplo y ejercicios.

La función parte entera de cualquier numero x es el entero mas grande que es menor o igual a x.

La parte entera de x esta denotada por [|x|]

Evalúa las siguientes expresiones.

a.[|2.3|] b.[|1.9|] c. [|0.1|] d.[|-0.3|]

      2          1            0          -1

e.[|-3.7|] f.[|3|] g.[|-2|] h.[|-0.999|]

      -3       3        -2           -1

Graficas de Funciones Basicas

Hoy estabamos familiarizandonos con las graficas de las funciones mas basicas, que de base, debemos de memorizarlas para hacer el proceso de aprendizaje mas facil en lo que es la introduccion al precalculo. Esta es la continuacion de las otras graficas que tocamos el 30 de agosto.

1. Funcion Cubica

Df=(-∞,∞)

Rf=(-∞,∞)

2. Funcion de Valor Absoluto

Df=(-∞,∞)

Rf=[0,∞)

3. Funcion Raiz Cuadrada

Df=[0,∞)

Rf=[0,∞)

4. Funcion Racional

Df=(-∞,0)U(0,∞)

Rf=(-∞,0)U(0,∞)

5. Funcion Raiz Cubica

Df=(-∞,∞)

Rf=(-∞,∞)

6. Funcion Constante

f(x) = b

Df=(-∞,∞)

Rf=[b]

Graficas de Funciones

El dia 30/agotso/2011 el maestro nos empezo a dar una breve descripcion de par de tipos de graficas junto a sus funciones, dominios y rangos. Las cuales son las siguientes:

A. Funcion Identidad:

. f(x)= x

B. Funcion Lineal:

f(x)= mx+b

C. Funcion Cuadratica:

René Descartes

La Haye, Francia, 1596 - Estocolmo, Suecia, 1650) Filósofo y matemático francés. René Descartes se educó en el colegio jesuita de La Flèche (1604-1612), donde gozó de un cierto trato de favor en atención a su delicada salud.
Obtuvo el título de bachiller y de licenciado en derecho por la facultad de Poitiers (1616), y a los veintidós años partió hacia los Países Bajos, donde sirvió como soldado en el ejército de Mauricio de Nassau. En 1619 se enroló en las filas del duque de Baviera; el 10 de noviembre, en el curso de tres sueños sucesivos, René Descartes experimentó la famosa «revelación» que lo condujo a la elaboración de su método. Los cinco primeros años los dedicó principalmente a elaborar su propio sistema del mundo y su concepción del hombre y del cuerpo humano, que estaba a punto de completar en 1633 cuando, al tener noticia de la condena de Galileo, renunció a la publicación de su obra, que tendría lugar póstumamente.
En 1637 apareció su famoso Discurso del método, presentado como prólogo a tres ensayos científicos. Descartes proponía una duda metódica, que sometiese a juicio todos los conocimientos de la época, aunque, a diferencia de los escépticos, la suya era una duda orientada a la búsqueda de principios últimos sobre los cuales cimentar sólidamente el saber. El método cartesiano, que Descartes propuso para todas las ciencias y disciplinas, consiste en descomponer los problemas complejos en partes progresivamente más sencillas hasta hallar sus elementos básicos, las ideas simples, que se presentan a la razón de un modo evidente, y proceder a partir de ellas, por síntesis, a reconstruir todo el complejo, exigiendo a cada nueva relación establecida entre ideas simples la misma evidencia de éstas. Los ensayos científicos que seguían, ofrecían un compendio de sus teorías físicas, entre las que destaca su formulación de la ley de inercia y una especificación de su método para las matemáticas. Los fundamentos de su física mecanicista, que hacía de la extensión la principal propiedad de los cuerpos materiales, los situó en la metafísica que expuso en 1641, donde enunció así mismo su demostración de la existencia y la perfección de Dios y de la inmortalidad del alma. El mecanicismo radical de las teorías físicas de Descartes, sin embargo, determinó que fuesen superadas más adelante.
Pronto su filosofía empezó a ser conocida y comenzó a hacerse famoso, lo cual le acarreó amenazas de persecución religiosa por parte de algunas autoridades académicas y eclesiásticas, tanto en los Países Bajos como en Francia. En 1649 aceptó la invitación de la reina Cristina de Suecia y se desplazó a Estocolmo, donde murió cinco meses después de su llegada a consecuencia de una neumonía. Descartes es considerado como el iniciador de la filosofía racionalista moderna por su planteamiento y resolución del problema de hallar un fundamento del conocimiento que garantice la certeza de éste, y como el filósofo que supone el punto de ruptura definitivo con la escolástica.

-GMRS

Continuacion de Dominio de Funciones

En el dia de hoy solo discutimos varios ejercicios de Dominio de Funciones .

El dominio es el conjunto de elementos que tienen imagen.

D = {x / f (x)}

El dominio (conjunto de definición o conjunto de partida ) de una función es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota o bien 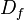y está definido por:

-LMA